CONTENIDO#6

Teorema del Seno

Sea un triángulo cualquiera con lados $a$, $b$ y $c$ y con ángulos interiores $\alpha$, $\beta$ y $\gamma$ (son los ángulos opuestos a los lados, respectivamente).

Entonces, se cumple la relación

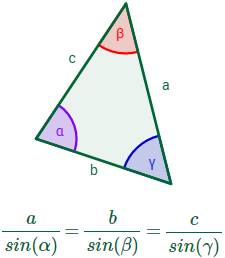
Además, se cumple

$$\frac{a}{sin\left(\alpha \right)}=D=2R$$

Representamos el triángulo circunscrito en una circunferencia de radio $R$ (diámetro $D=2R$) y de centro $o$.
Representamos otro triángulo de modo que:

• uno de sus lados coincide con uno de los lados del triángulo inicial, por ejemplo, el lado $b$.
• es un triángulo rectángulo, es decir, uno de sus ángulos mide 90º. Para dicho ángulo, nosotros hemos escogido el vértice donde está el ángulo $\alpha$.

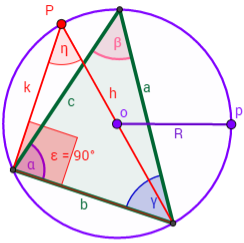El triángulo tiene otros dos lados: $k$ y $h$. El lado $h$ es su hipotenusa y puesto que pasa por el centro de la circunferencia, mide exactamente lo mismo que el diámetro:

$$h=D=2\cdot R$$

Se cumple que los ángulos $\eta$ y $\beta$ son iguales y, por tanto, también lo son sus senos:

$$sin\left(\eta \right)=sin\left(\beta \right)$$

Y como el nuevo triángulo es rectángulo,

$$sin\left(\beta \right)=sin\left(\eta \right)=\frac{b}{h}$$

Luego

$$h=\frac{b}{sin\left(\beta \right)}$$

Como $h=D=2R$,

$$2R=\frac{b}{sin\left(\beta \right)}$$

De forma similar, se obtienen las relaciones

$$2R=\frac{a}{sin\left(\alpha \right)}$$

$$2R=\frac{c}{sin\left(\gamma \right)}$$

de donde se concluye el teorema.