Movimiento Circular Uniforme
(M.C.U.)
El movimiento circular uniforme (MCU) es el movimiento que describe una partícula cuando da vueltas sobre un eje estando siempre a la misma distancia (r) del mismo y desplazándose a una velocidad constante.
Posición
La posición de la partícula depende de su posición inicial y de la velocidad a la que se desplaza. Ésta se puede calcular a partir del incremento angular, de la velocidad angular y de la velocidad tangencial (en caso de conocer las velocidades es necesario saber el tiempo t que se ha movido el cuerpo o partícula).
Posición según el incremento del ángulo
ANUNCIOS
Podemos calcular la posición de la partícula a partir del incremento del ángulo:
En coordenadas cartesianas tenemos:


Posición según la velocidad angular
La posición de la partícula se puede calcular a partir de la velocidad angular y el tiempo
En coordenadas cartesianas tenemos:


Posición según la velocidad tangencial
También se puede calcular la posición de la partícula a partir de la velocidad tangencial
En coordenadas cartesianas tenemos:
Nota: Las unidades del ángulo son siempre en radianes.
Velocidad angular
En el MCU, la velocidad angular se puede calcular a partir del período o la frecuencia, ya que el período y la frecuencia son constantes.
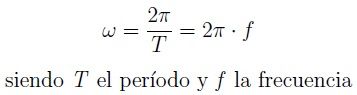
Otra forma de determinar la velocidad angular es:

Las unidades en las que se mide la velocidad angular ω es en radianes/seg, o simplemente en s-1.
La velocidad angular en el MCU es constante.
Velocidad tangencial
La velocidad tangencial es igual a la velocidad angular por el radio.

La velocidad tangencial, al igual que la velocidad angular, en el MCU es constante.
Aceleración centrípeta
A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de la velocidad se mantiene constante, el vector cambia constantemente de dirección. Ésta se calcula como:


Aceleración angular y tangencial
En el movimiento circular uniforme (MCU), tanto la aceleración angular como la aceleración tangenciales son cero.
Período
La velocidad angular en el MCU es constante, por lo que el período también será constante e irá definido por la fórmula siguiente:

Frecuencia
La frecuencia es constante al ser constante la velocidad angular y el período:

Ejercicio
Una rueda gira a una velocidad constante de 120 revoluciones por minuto (r.p.m.). Hallar:
- La frecuencia en ciclos/segundo.
- La velocidad angular en radianes/segundo.
- La velocidad tangencial en un punto de la rueda situado a 15 cm. del eje.
- Las aceleraciones tangenciales y centrípetas en el punto citado.
Solución:
- La frecuencia en ciclos/segundo se calcula dividiendo las r.p.m. entre los 60 segundos que tiene un minuto:

- La velocidad angular (ω):

- La velocidad tangencial en un punto de la rueda situado a 15 cm del eje, el radio de rotación será de r=15 cm, por lo tanto:

- La aceleración tangencial es 0:
 La aceleración centrípeta en el punto citado es:
La aceleración centrípeta en el punto citado es:
No hay comentarios.:
Publicar un comentario